Tutaj podaję odpowiedzi do mojego ostatniego posta:))
1) Korzystając z twierdzenia Pitagorasa w trójkątach prostokątnych zaznaczonych liniami przerywanymi obliczamy długości boków prostokąta.
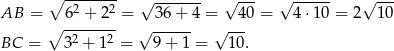
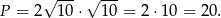
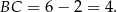
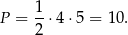
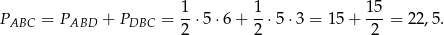
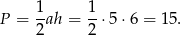
1) Korzystając z twierdzenia Pitagorasa w trójkątach prostokątnych zaznaczonych liniami przerywanymi obliczamy długości boków prostokąta.
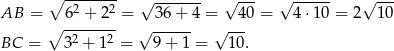
Zatem pole prostokąta jest równe
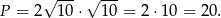
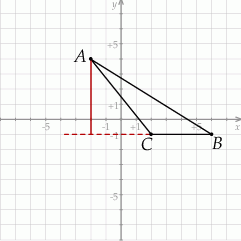
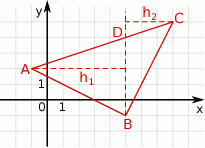
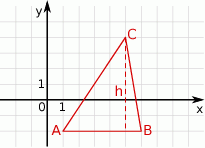
2) Zaczynamy od rysunku

Ponieważ odcinek 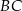 jest równoległy do osi
jest równoległy do osi 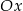 , ma on długość
, ma on długość
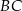 jest równoległy do osi
jest równoległy do osi 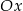 , ma on długość
, ma on długość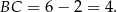
Wysokość opuszczona na ten bok ma długość 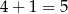 . Zatem pole jest równe
. Zatem pole jest równe
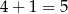 . Zatem pole jest równe
. Zatem pole jest równe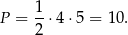
3)

Otrzymane trójkąty mają wspólną podstawę 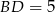 i wysokości równe
i wysokości równe 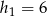 ,
, 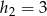 . W takim razie pole trójkąta
. W takim razie pole trójkąta 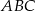 jest równe
jest równe
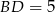 i wysokości równe
i wysokości równe 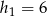 ,
, 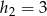 . W takim razie pole trójkąta
. W takim razie pole trójkąta 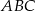 jest równe
jest równe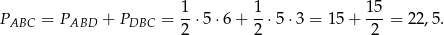
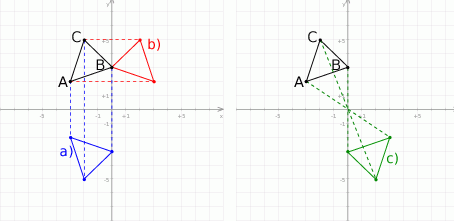
4)

a) 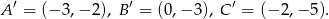
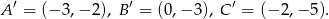
b) 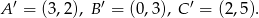
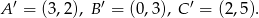
c) 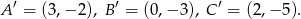
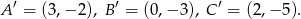
5) Wzór na pole trójkąta to 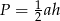 , gdzie a jest długością podstawy, na którą opuszczono wysokość.
, gdzie a jest długością podstawy, na którą opuszczono wysokość.
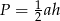 , gdzie a jest długością podstawy, na którą opuszczono wysokość.
, gdzie a jest długością podstawy, na którą opuszczono wysokość.
W naszej sytuacji a = |AB| = 5 i h = 6, więc pole jest równe
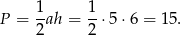
Komentarze
Prześlij komentarz