Tutaj zamieszczam odpowiedzi do mojego ostatniego posta
1)
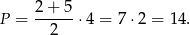
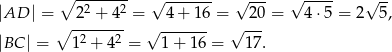
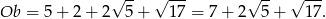
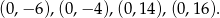
1)

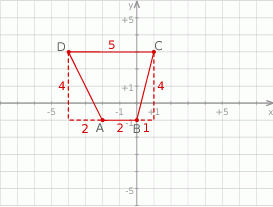
Otrzymany czworokąt to trapez o podstawach długości 2 i 5, oraz wysokości równej 4. Jego pole jest więc równe
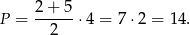
Aby obliczyć obwód tego trapezu korzystamy z twierdzenia Pitagorasa w trójkątach prostokątnych zaznaczonych przerywanymi liniami.
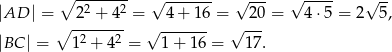
Obwód trapezu jest więc równy
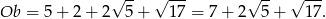
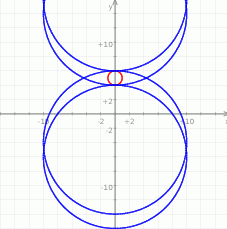
2) Jeżeli naszkicujemy sobie opisaną sytuację, to widać, że mogą być cztery takie okręgi: dwa styczne zewnętrznie i dwa styczne wewnętrznie.

Aby wyznaczyć ich środki wystarczy skorzystać z faktu, że odległość środków okręgów stycznych zewnętrznie jest równa sumie ich promieni, a w przypadku okręgów stycznych wewnętrznie, odległość ta jest różnicą promieni.
Łatwo wyznaczyć wszystkie cztery możliwe środki:
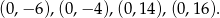
Komentarze
Prześlij komentarz